


Next: Current calculation
Up: Details of the Calculations
Previous: Details of the Calculations
Contents
When we compile the SKKR program we should pay attention to the parameters
used in the
program. The parameters to be changed can be found in the files 'inc.p' and
'inc.cls'.
First we will start from the inc.cls file. There are mainly two parameters
someone would take care of. The first one is the NACLSD which is the number of
atoms in the tight-binding cluster used for the screening.
Normally for a bulk calculation first-second neighbors at least are needed
to have good results. Convergence of different properties is different with
the cluster size, and should be checked.
The second parameter is the NCLSD which is the number of different clusters
used in the calculation (look at the part on the VORONOI for more details).
Now we will just mention the parameters to be changed each time we compile the
KKR program in the inc.p file. Parameters
NATYPD and NAEZD are equal to
the total number of atoms used in the calculation.
LMAXD is
the 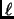 -cut-off for the wave functions.
-cut-off for the wave functions.
NSPIND is the number of spins: 1 for a paramagnetic calculation
and 2 for a spin-polarized one.
IRMD is the total number of points in the radial mesh
and should be larger or equal to the IRM parameter in the inputcard.
IEMXD is the number of points in complex energy plane for the integration
and should be larger than the sum npt1+npt2+npt3 in the inputcard.
IRNSD
is the number of points where the potential is non-spherical and should be at
least equal to the IRNS in the inputcard.
NEMBD is the
number of embedding positions around the real atomic positions when we do a
calculation with a 2D geometry. attention that we should take into account
both left and right hosts. For example in the case of the 001 surface of an
one-element fcc
crystal we have one embedded position from each site so NEMBD=2.
If we had two inequivalent atoms per
layer then NEMBD=4.
NPRINCD should be set to 1 unless we use principal layers
(usually for DECIMATION), then it has to be set to the correct value.
NAUXSPD is for sparse matrix inversion, if you use sparse option
the program might stop asking you to increase this.
NSHELLD is the number of GF blocks that will be used. For SC calculation
this is equal to the NATYPD, since only the Green's function diagonal is
needed, but for impurity GF or current calculation it must be increased. The
program will stop asking for this.
NSYMD is the number of symmetry operations, it is usually set to 48 but for
low symmetry systems you have big NSHELLD so it can be reduced to the
to save memory.
NATOMIMPD is the number of impurity atoms we want a GR for.
The rest of the parameters are self-explanatory or they are not changed
to often, change only when program stops asking for change.
In all the above cases the program stops if a parameter
is wrong and we should look at the end of the output file to see which
parameter is wrong.
Matrix dimensions
Current version includes 3 main matrix inversion modes.
full inv: Inversion using LU decomposition.
sparse: Sparse matrix inversion.
If no option exists a block matrix inversion is used. The method supposes that
the matrix is non-zero only in the diagonal, upper-diagonal, lower-diagonal.
The matrix is transformed in this form by grouping the rows and columns in
principal layers. In order to divide the matrix its size,
(i.e. total number of layers) should be exactly divided by the number of
layers in each principal layer NPRINCD. This number is given
in the parameters file inc.p and should be set correctly
or RESULTS COULD BE WRONG.
How to decide on the size of the principal layer!
The program calculates and prints out the Dyson equation
matrix in the form 1. To find the size of the principal layer
you draw a line which passes through the last coupled layers (last ones)
as illustrated in the figure.
Figure 2:
Form of the Dyson equation, and the principal layer concept
each 0 and 1 correspond to an LMMAX x LMMAX matrix (i.e. LMMAX=16 for
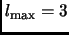 ).
The line demonstrates a simple way to find the size of the
principal layers which is 5 in this example
).
The line demonstrates a simple way to find the size of the
principal layers which is 5 in this example
|
|



Next: Current calculation
Up: Details of the Calculations
Previous: Details of the Calculations
Contents
Nikos Papanikolaou
2002-11-08
![\includegraphics[scale=1.0]{deciexamp.eps}](img57.png)